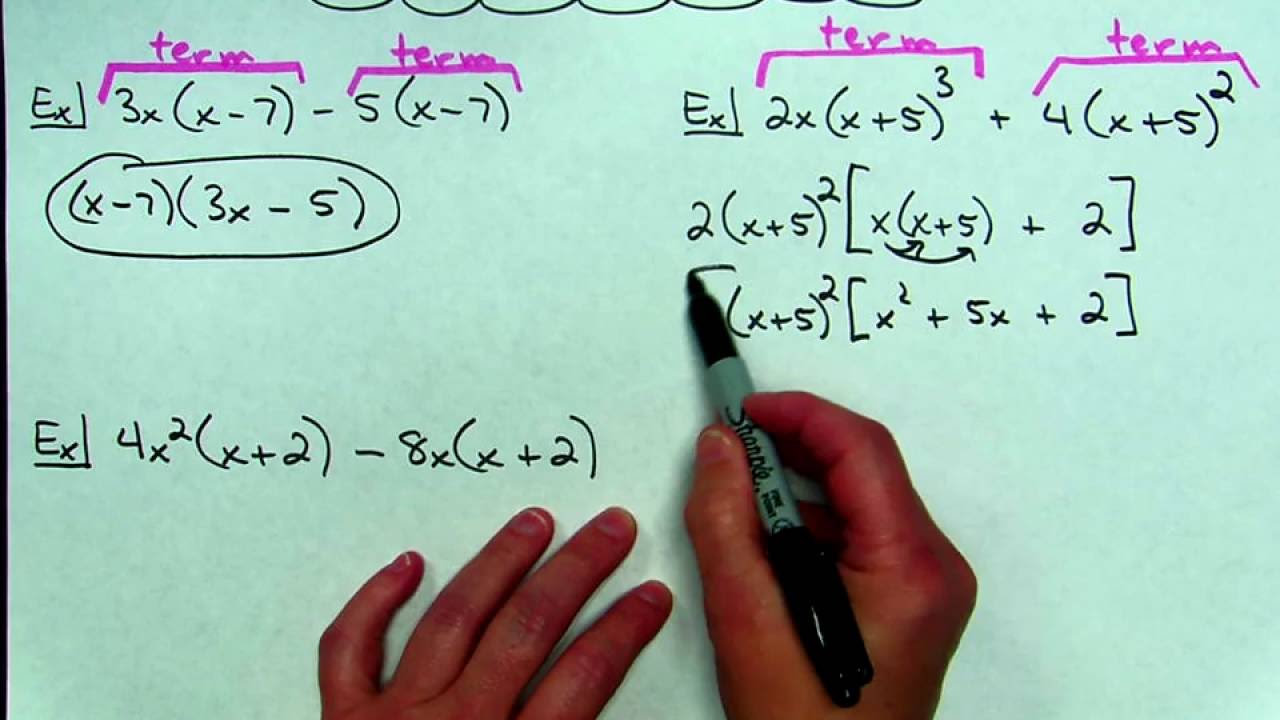
How To Factor By Grouping 4 Terms Calculator?

Read Time:4 Minute, 48 Second

Factoring polynomials with four terms can be greatly simplified by using an online calculator to factor by grouping. Start by inputting the four term expression as one polynomial – for example 2x^2+5x+3x+6.

The calculator will then automatically split this into two groups of terms – grouping (2x^2+5x) and (3x+6). It identifies the GCF in each group and factors this out, leaving (2x(x+5)) and (3(x+2)).

Finally, the calculator factors out the common factor between these groupings, which is (x+2), leaving the fully factored form: (x+2)(2x+3). Rather than working through each conceptual step manually, the calculator does the heavy lifting.

In just a few seconds, you can utilise the factor by grouping method to take any four term polynomial and simplify it into the reduced, factored format by harnessing the power of an online tool.

What Types Of Polynomials Can I Factor With A 4 Term Calculator?

A 4 term factoring calculator can factor any polynomial that has specifically 4 terms. This includes quadratic polynomials that can be factored into the form (ax + b)(cx +d). Polynomials must have a degree of 2 or less.

Only expressions with 4 individual terms separated can be factored. Polynomials with more or less than 4 terms cannot be processed. The calculator performs factoring by grouping on valid 4 term, quadratic polynomial input.

Do 4 Term Factoring Calculators Work For All Expressions?

No, 4 term factoring calculators do not work for all mathematical expressions. These specialised calculators are designed specifically to factor polynomials that contain exactly 4 terms using the factoring by grouping method.

The calculators take advantage of the fact that 4 term polynomial expressions can always be split into two groups of 2 terms each. From there, the greatest common factor is pulled out of each group, and then the final common factor between the two groupings is used to arrive at the fully factored form.

However, the calculators have limitations:

They can only process valid polynomials that have 4 distinct, separated terms connected by addition or subtraction. Expressions with less than or greater than 4 terms will not factor properly.

The polynomials must have a degree of 2 or less. Typically, they factor quadratic expressions that resolve into the form (ax + b)(cx + d).

There are likely restrictions on the types of variable names/letters and limitations to coefficient sizes due to overflow errors.

Expressions formatted incorrectly or with anything other than 4 individual terms will either produce an error or inaccurate factorization.

So while extremely useful for factoring 4 term polynomial expressions through grouping, these calculators do not provide universal factoring capabilities. General maths software would be needed to attempt to factor broader algebraic expressions. For the specific purpose they are designed for though, 4 term factoring calculators dramatically simplify the process.

How Do I Input My 4 Term Polynomial Into The Calculator?

Type the 4 terms separated by addition or subtraction signs, like x^2+5x+3+4 or 2x^2-3x-2+4x, using the allowed variables and coefficients. Do not include spaces or other terms.

Ensure proper order of operations is followed as you input your expression to be factored. Groupings such as parentheses should not be included in the input polynomial.

Will The Calculator Show The Step-By-Step Work For Factoring?

No, most 4 term factoring calculators will not display the step-by-step work. They are designed to take the 4 term polynomial input and output only the final factored form. For details on the factoring by grouping process used to arrive at the solution.

You’ll need to understand the conceptual steps behind the scenes or use maths software that shows full work. But these specialised calculators simplify implementation by handling the factoring work internally and skipping straight to the final factored format of your polynomial.

Can I Factor Polynomials With Coefficients Other Than 1 On These Calculators?

When working with factoring polynomials, it is common to start with examples that have simple integer coefficients of 1. However, most polynomial functions have coefficients with values other than 1.

Thankfully, many scientific and graphing calculators have built-in features for factoring polynomials with any rational number coefficients. For example, on TI-84 Plus graphing calculators, you can use the “factor()” function under the Math menu which will factor quadratic, cubic, and quartic polynomial expressions with numeric rational coefficients.

The key requirement is that the lead coefficient cannot be 0. This makes factoring polynomials with coefficients other than 1 just as convenient as factoring simple expressions.

Understanding how to fully utilise these tools prepares students for more complex polynomial factoring needed in calculus and beyond. Having the unit circle chart handy with trig function values at key angles is another useful mathematical reference when evaluating and graphing factored polynomial functions.

Making use of all available maths tools, from calculator capabilities to helpful charts, allows students to take on more advanced problems.

Is There A Restriction On The Degree Of The Polynomials It Can Factor?

Most graphing calculators have built-in functions for easily factoring polynomials, but they are limited to expressions with degree 4 or less. This means only quadratic, cubic, and quartic polynomials can be directly factored using the calculator tools.

The reason for the degree restriction is because there are no general algebraic formulas for factoring polynomials of degree 5 or higher. While those higher degree polynomials may still have rational factors, testing the infinite possibilities to find them is beyond computing capabilities.

By supporting factorization for polynomials of degree up to 4, graphing calculators cover the most common polynomial factoring needs using established algebraic procedures. But users should be aware that attempting to factor quintics or higher will exceed the graphing calculator’s capabilities.